Hur gissningar påverkar gränsen för godkänt
Risken med quizfrågor med givna svarsalternativ är att studenterna kan gissa sig till korrekt svar på frågorna. För att kunna mäta studenternas faktiska kunskapsnivåer måste du ta hänsyn till gissningar när du sätter gränserna för godkänt. Här utgår vi från en vetenskaplig artikel av Brett P. Foley för att beräkna denna risk och ger förslag på hur du kan hantera den.
Sannolikheten att gissa sig till godkänt
Anta att du har ett quiz med 20 frågor i formen av "flera svarsalternativ" (multiple choice) med ett korrekt svarsalternativ. Sannolikheten att studenter gissar rätt på en fråga beror på antalet svarsalternativ, men vad är sannolikheten för att de gissar rätt på flera frågor?
För att besvara frågan utgår vi från Foley, Brett P. (2019) "Getting Lucky: How Guessing Threatens the Validity of Performance Classifications". Speciellt beräkningarna i Appendix A, om vad sannolikheten är att en student uppnår ett visst antal rätta svar på ett quiz genom att bara gissa. Sannolikheterna för frågor med två, tre, fyra och fem svarsalternativ listas i Tabell 1 och visas även i Diagram 1.
Obs! Vi har antagit att alla svarsalternativ är lika troliga. Det vill säga, de felaktiga svarsalternativen är troliga och formulerade liknande som det korrekta svarsalternativet. Läs mer om att Formulera frågor och svarsalternativ .
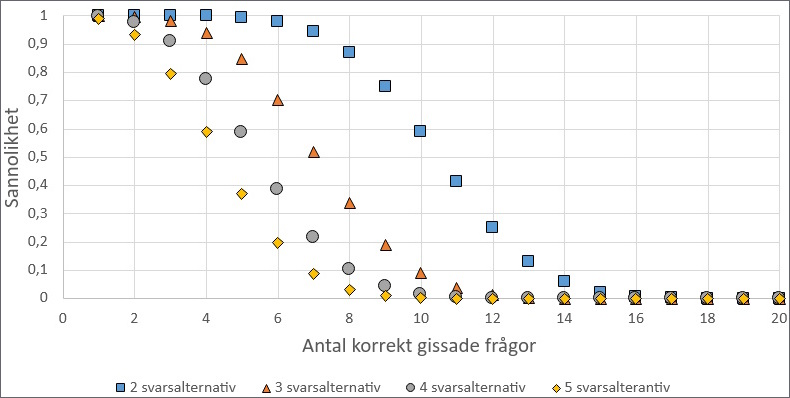
En student är nästan garanterad att gissa rätt på en eller två frågor oavsett antalet svarsalternativ, men sannolikheten sjunker snabbare ju fler svarsalternativ per fråga. För fyra och fem svarsalternativ är det väldigt låg sannolikhet att någon gissar korrekt på fler än 8 eller 9 frågor. För tre svarsalternativ är det närmare 11 och med bara två svarsalternativ är det runt 15 frågor.
| Antal korrekt gissade frågor | 2 svarsalternativ (%) | 3 svarsalternativ (%) | 4 svarsalternativ (%) | 5 svarsalternativ (%) |
|---|---|---|---|---|
| 1 |
100 |
99,97 |
99,68 |
98,85 |
| 2 |
100 |
99,67 |
97,57 |
93,08 |
| 3 |
99,98 |
98,24 |
90,87 |
79,39 |
| 4 |
99,87 |
93,96 |
77,48 |
58,86 |
| 5 |
99,41 |
84,85 |
58,52 |
37,04 |
| 6 |
97,93 |
70,28 |
38,28 |
19,58 |
| 7 |
94,23 |
52,07 |
21,42 |
8,67 |
|
8 |
86,84 |
33,85 |
10,18 |
3,21* |
| 9 |
74,83 |
19,05 |
4,09* |
1,00 |
| 10 |
58,81 |
9,19 |
1,39 |
0,26 |
| 11 |
41,19 |
3,76* |
0,39 |
0,06 |
| 12 |
25,17 |
1,30 |
0,09 |
0,01 |
| 13 |
13,16 |
0,37 |
0,02 |
0 |
| 14 |
5,77 |
0,09 |
0 | 0 |
| 15 |
2,07* |
0,02 |
0 | 0 |
| 16 |
0,59 |
0 | 0 | 0 |
| 17 |
0,13 |
0 | 0 | 0 |
| 18 |
0,02 |
0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 0 |
Att tänka på när du sätter omdömesgränserna
Risken är aldrig noll för att en student gissar alla rätt på ett quiz, men den blir försvinnande liten vid längre quiz. Brett P Foley använder sig av 5% sannolikhet som den minimala gränsen för godkänt, men föreslår även gränserna 10% eller 1% beroende på vikten av quizet. Den minimala gränsen är dock bara ett minimumvärde att hålla sig ovanför, det är inte den rekommenderade gränsen för godkänt. Information om hur du kan justera gränsen för godkänt hittar du sist på sidan.
I det tidigare exemplet använde vi oss av ett quiz med 20 frågor, men ett quiz med få frågor gör att omdömesskalan blir väldigt smal. Till exempel, om du använder dig av tre svarsalternativ skulle varje omdöme på skalan A till E motsvara två frågor var. Studenterna får inget utrymme att göra misstag och du måste skapa ett quiz som reflekterar en så snäv skala. Därför rekommenderar vi att du förlänger quiz med få svarsalternativ eller att du använder en enklare omdömesskala, exempelvis Godkänt/Ej godkänt.
Som ett exempel på ett långt quiz har vi skapat listor över de minimala gränserna för 1%, 5% och 10% för ett quiz med 100 frågor.
Möjliga problem med modellen
Vi har utgått från vissa antaganden i våra beräkningar som förklaras i detalj i artikeln av Brett P Foley. Det kan dock uppstå problem med modellen när dessa antaganden inte är uppfyllda. Brett P Foley hittar exempelvis dessa problem:
- Studenter kan skippa frågor i stället för att gissa. Om du har höjt omdömesgränserna för att motverka gissningar och inga gissningar sker, så kommer den studenten få svårare att få godkänt.
- Studenter kan ha delkunskap som gör att de kan utesluta svarsalternativ och sen gissa. Till exempel kanske en student inte vet vilket svarsalternativ som är korrekt men vet att ett av dem är garanterat inkorrekt. Då är det större sannolikhet att studenten gissar rätt än modellen säger.
Metoder för att justera gränsen för godkänt
Det finns många artiklar om de olika sätten att justera gränsen för godkänt på quiz. Brett P Foley tar upp följande formel i Appendix D för att räkna ut den justerade gränsen för godkänt (Xadj):
\(X_{adj} = X_{raw} + [P*L*(X_{max} - X_{raw})]\)
Xraw är poängen för den ojusterade gränsen för godkänt.
Xmax är högsta poängen man kan få på quizet.
P är sannolikheten att gissa rätt per fråga (baseras på antalet svarsalternativ).
L är sannolikheten att en student gissa på en fråga när de inte kan svaret. Brett P Foley förklarar hur detta kan uppskattas i Appendix D utifrån beräkningar i Appendix C.
Följande artiklar är några andra exempel på sätt att hantera bedömning av quiz när studenter kan gissa sig till rätt svar. Detta är endast ett urval, den intresserade rekommenderas att söka upp fler artiklar.
- Formula Scoring of Multiple-Choice Tests (Correction for Guessing) (engelska, onlinelibrary.wiley.com) .
- Optimal Correction for Guessing in Multiple-Choice Tests (engelska, researchgate.net) .
